Решение #zoda4a (vk.com/wall14_71431)
Если стоимость жилья растет на 3% в год, а уменьшается на 1% и потом чуть больше, чем на 1%, то сперва стоимость жилья растет, а после какого-то момента падает
Пусть цена в какой-то год X(n)
Рост цены на 3% приведет к тому, что цена станет равна x(n)*1.03, а чтобы выразить падение цены, заметим, что в первый год она падает на 1/100, то есть остается 99/100, во второй на 1/99, то есть остается 98/99, на третий 97/98 и тд.
Получается, что в год с номером n цена изменится в (100-n)/(101-n) раз, и для цены в n+1 год мы получаем
x(n+1)=x(n)*1.03*(100-n)/(101-n)
если x(n+1)>x(n), цена растет
если x(n+1)<x(n), цена падает
Найдем, начиная с какого номера цена начнет падать - он и покажет, когда у дома была максимальная стоимость.
x>x*1.03*(100-n)/(101-n)
x положительный, на него можно сократить =)
101-n>103-1.03*n
0.03n>2
n>66.(66)
значит, на 66 год цена будет максимальной.
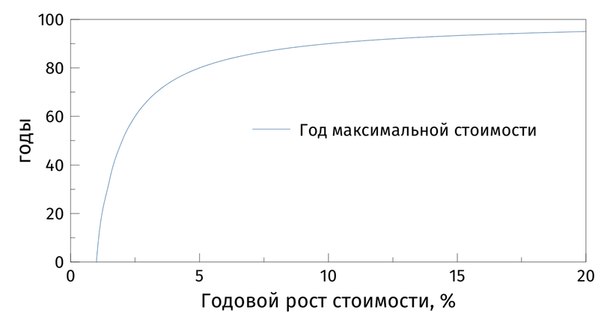
Интересно, как этот год зависит от степени роста стоимости жилья — на картинке график зависимости года от роста цены в процентах. Год максимальной стоимости от нулевого до 80 года взлетает буквально за 4% — c 1% до 5%, а дальше уже медленно асимптотически (то есть никогда не пересекая) ползёт к 100 годам, то есть всему сроку лиза.
график легко и быстро построен в [club1872310|MagicPlot]
Если стоимость жилья растет на 3% в год, а уменьшается на 1% и потом чуть больше, чем на 1%, то сперва стоимость жилья растет, а после какого-то момента падает
Пусть цена в какой-то год X(n)
Рост цены на 3% приведет к тому, что цена станет равна x(n)*1.03, а чтобы выразить падение цены, заметим, что в первый год она падает на 1/100, то есть остается 99/100, во второй на 1/99, то есть остается 98/99, на третий 97/98 и тд.
Получается, что в год с номером n цена изменится в (100-n)/(101-n) раз, и для цены в n+1 год мы получаем
x(n+1)=x(n)*1.03*(100-n)/(101-n)
если x(n+1)>x(n), цена растет
если x(n+1)<x(n), цена падает
Найдем, начиная с какого номера цена начнет падать - он и покажет, когда у дома была максимальная стоимость.
x>x*1.03*(100-n)/(101-n)
x положительный, на него можно сократить =)
101-n>103-1.03*n
0.03n>2
n>66.(66)
значит, на 66 год цена будет максимальной.
Интересно, как этот год зависит от степени роста стоимости жилья — на картинке график зависимости года от роста цены в процентах. Год максимальной стоимости от нулевого до 80 года взлетает буквально за 4% — c 1% до 5%, а дальше уже медленно асимптотически (то есть никогда не пересекая) ползёт к 100 годам, то есть всему сроку лиза.
график легко и быстро построен в [club1872310|MagicPlot]
Solution # zoda4a (vk.com/wall14_71431)
If the cost of housing rises by 3% per year, and decreases by 1% and then slightly more than 1%, then at first the cost of housing rises, and after a certain moment it falls
Let the price in some year X (n)
A 3% price increase will lead to the price being equal to x (n) * 1.03, and to express a price drop, we note that in the first year it falls by 1/100, that is, 99/100, in the second by 1 / 99, that is, 98/99 remains, the third 97/98 and so on.
It turns out that in the year with the number n the price will change (100-n) / (101-n) times, and for the price in n + 1 year we get
x (n + 1) = x (n) * 1.03 * (100-n) / (101-n)
if x (n + 1)> x (n), the price rises
if x (n + 1) <x (n), the price falls
We will find, starting from what number the price starts to fall - it will show when the house had a maximum value.
x> x * 1.03 * (100-n) / (101-n)
x positive, it can be reduced =)
101-n> 103-1.03 * n
0.03n> 2
n> 66. (66)
It means that at 66 the price will be maximum.
I wonder how this year depends on the degree of growth in the cost of housing - in the picture is a graph of the year’s dependence on price growth in percent. The year of the maximum cost from zero to 80 takes off literally in 4% - from 1% to 5%, and then slowly asymptotically (that is, never crossing) crawls to 100 years, that is, the entire term of the lease.
schedule quickly and easily built in [club1872310 | MagicPlot]
If the cost of housing rises by 3% per year, and decreases by 1% and then slightly more than 1%, then at first the cost of housing rises, and after a certain moment it falls
Let the price in some year X (n)
A 3% price increase will lead to the price being equal to x (n) * 1.03, and to express a price drop, we note that in the first year it falls by 1/100, that is, 99/100, in the second by 1 / 99, that is, 98/99 remains, the third 97/98 and so on.
It turns out that in the year with the number n the price will change (100-n) / (101-n) times, and for the price in n + 1 year we get
x (n + 1) = x (n) * 1.03 * (100-n) / (101-n)
if x (n + 1)> x (n), the price rises
if x (n + 1) <x (n), the price falls
We will find, starting from what number the price starts to fall - it will show when the house had a maximum value.
x> x * 1.03 * (100-n) / (101-n)
x positive, it can be reduced =)
101-n> 103-1.03 * n
0.03n> 2
n> 66. (66)
It means that at 66 the price will be maximum.
I wonder how this year depends on the degree of growth in the cost of housing - in the picture is a graph of the year’s dependence on price growth in percent. The year of the maximum cost from zero to 80 takes off literally in 4% - from 1% to 5%, and then slowly asymptotically (that is, never crossing) crawls to 100 years, that is, the entire term of the lease.
schedule quickly and easily built in [club1872310 | MagicPlot]
У записи 3 лайков,
0 репостов.
0 репостов.
Эту запись оставил(а) на своей стене Андрей Городецкий























