Прошедшая на прошлой неделе #ЗПШ_СПБГУ для меня, пожалуй, была лучшей из всех, на которых я побывал. Отчасти потому, что я сам решил подойти к своей лекции "по-научному": выбрал тему на стыке психологии, математики и финансов, и даже попытался воспроизвести эффект "underreaction/overreaction" (Barberis et al., 1998), для чего провёл мини-эксперимент. Если вы ещё не проходили этот опрос, советую его пройти (bit.ly/pgi-math): он короткий, а читать дальше будет интереснее.
Вводный текст для опроса выглядит так.
У меня есть две монеты. Первая (назовём её орлово-ориентированной) выпадает орлом в 70% случаев, решкой в 30%. Вторая — решко-ориентированная — ровно наоборот: 70% решка, 30% орёл.
Я прячу монеты и выбираю одну из них наугад. Эту монету я буду подкидывать и сообщать результаты вам. Оставшаяся не выбранная мной монета в эксперименте более не участвует.
На каждом шаге я сообщаю результат следующего броска. Ваша задача: оценить вероятность того, что я подбрасываю орлово-ориентированную монету.
Далее участнику или участнице последовательно сообщаются результаты бросков. Это серия 1:орёл, 2:орёл, 3:орёл, 4:орёл, 5:орёл, 6:решка.
В тексте также говорится, что не существует понятия "неправильной" оценки, поскольку процедура оценивания — субъективный процесс. Если бы мы были абсолютно рациональны, то мы сначала выбирали бы процедуру оценивания (оптимальную в каком-то строго определённом смысле), а потом использовали её, не меняя на другую с приходом новой информации. Один из таких способов оценивания — использование формулы Байеса. Байесовцы рассуждают примерно так: если подкидываний ещё не было, то шансы 50 на 50. Если в серии подкидываний намного больше орлов, например 3 орла и ни одной решки, будет ли оценка орлово-ориентированности по-прежнему 50%? Нет, потому что такой исход эксперимента более вероятен для орлово-ориентированной монеты, нежели чем для решко-ориентированной. Таким образом, чем больше дисбаланс между количеством орлов и решек, тем больше мы можем быть уверены в том, какая монета была выбрана. (Если этот аргумент неубедителен, попробуйте заменить 70%/30% на 99%/1% для обеих монет и повторить рассуждение.)
В этом рассуждении и состоит суть формулы Байеса: вероятность наступления события при условии имеющейся информации P(A|B) выражается как P(B|A)*P(A)/P(B). Здесь в нашем случае A означает событие "орлово-ориентированность выбранной наугад монеты", B — "история наблюдаемых бросков" (она меняется на каждом шаге эксперимента). Остальное — дело техники. Вывод формулы в общем виде для n орлов и m решек довольно прост, особенно если учесть, что P(A)=0.5. Приведу окончательный результат: P(A|B) = 0.7^n * 0.3^m / (0.7^n * 0.3^m + 0.7^m * 0.3^n). Применение этой формулы даёт ответы "полностью рационального Байесовца": 70%, 84.5%, 92.7%, 96.7%, 98.6%, 96.7%.
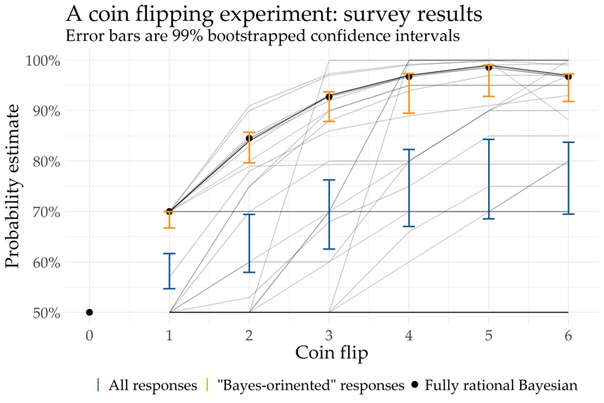
Ну а теперь посмотрим на экспериментальные данные! Каждая чёрная траектория обозначает одну серию ответов. Если траектории накладываются, линия становится менее прозрачной. Наиболее популярны три категории ответов: все оценки 50% (новая информация не влияет никак), все оценки 70% (по-видимому, влияет только тот факт, что орлов больше), а также оценивание по Байесу (эта группа точно использовала формулу Байеса — без вычисления попасть в эту траекторию очень трудно). Ну а в среднем (синий цвет) оценки похожи по форме на Байесовские, но они сильно занижены. Это можно условно обоначить как эффект underreaction. Если посмотреть на среднее, исключив траектории "все 50%"/"все 70%" (оранжевый цвет), то здесь доверительный интервал с уровнем доверия 99% накрывает Байесовскую траекторию. Эффекта overreaction, к которому апеллируют авторы оригинальной статьи, обнаружить не удалось. Science is hard!
Ссылки на презентацию и код, пожалуй, выложу следующим постом.
Вводный текст для опроса выглядит так.
У меня есть две монеты. Первая (назовём её орлово-ориентированной) выпадает орлом в 70% случаев, решкой в 30%. Вторая — решко-ориентированная — ровно наоборот: 70% решка, 30% орёл.
Я прячу монеты и выбираю одну из них наугад. Эту монету я буду подкидывать и сообщать результаты вам. Оставшаяся не выбранная мной монета в эксперименте более не участвует.
На каждом шаге я сообщаю результат следующего броска. Ваша задача: оценить вероятность того, что я подбрасываю орлово-ориентированную монету.
Далее участнику или участнице последовательно сообщаются результаты бросков. Это серия 1:орёл, 2:орёл, 3:орёл, 4:орёл, 5:орёл, 6:решка.
В тексте также говорится, что не существует понятия "неправильной" оценки, поскольку процедура оценивания — субъективный процесс. Если бы мы были абсолютно рациональны, то мы сначала выбирали бы процедуру оценивания (оптимальную в каком-то строго определённом смысле), а потом использовали её, не меняя на другую с приходом новой информации. Один из таких способов оценивания — использование формулы Байеса. Байесовцы рассуждают примерно так: если подкидываний ещё не было, то шансы 50 на 50. Если в серии подкидываний намного больше орлов, например 3 орла и ни одной решки, будет ли оценка орлово-ориентированности по-прежнему 50%? Нет, потому что такой исход эксперимента более вероятен для орлово-ориентированной монеты, нежели чем для решко-ориентированной. Таким образом, чем больше дисбаланс между количеством орлов и решек, тем больше мы можем быть уверены в том, какая монета была выбрана. (Если этот аргумент неубедителен, попробуйте заменить 70%/30% на 99%/1% для обеих монет и повторить рассуждение.)
В этом рассуждении и состоит суть формулы Байеса: вероятность наступления события при условии имеющейся информации P(A|B) выражается как P(B|A)*P(A)/P(B). Здесь в нашем случае A означает событие "орлово-ориентированность выбранной наугад монеты", B — "история наблюдаемых бросков" (она меняется на каждом шаге эксперимента). Остальное — дело техники. Вывод формулы в общем виде для n орлов и m решек довольно прост, особенно если учесть, что P(A)=0.5. Приведу окончательный результат: P(A|B) = 0.7^n * 0.3^m / (0.7^n * 0.3^m + 0.7^m * 0.3^n). Применение этой формулы даёт ответы "полностью рационального Байесовца": 70%, 84.5%, 92.7%, 96.7%, 98.6%, 96.7%.
Ну а теперь посмотрим на экспериментальные данные! Каждая чёрная траектория обозначает одну серию ответов. Если траектории накладываются, линия становится менее прозрачной. Наиболее популярны три категории ответов: все оценки 50% (новая информация не влияет никак), все оценки 70% (по-видимому, влияет только тот факт, что орлов больше), а также оценивание по Байесу (эта группа точно использовала формулу Байеса — без вычисления попасть в эту траекторию очень трудно). Ну а в среднем (синий цвет) оценки похожи по форме на Байесовские, но они сильно занижены. Это можно условно обоначить как эффект underreaction. Если посмотреть на среднее, исключив траектории "все 50%"/"все 70%" (оранжевый цвет), то здесь доверительный интервал с уровнем доверия 99% накрывает Байесовскую траекторию. Эффекта overreaction, к которому апеллируют авторы оригинальной статьи, обнаружить не удалось. Science is hard!
Ссылки на презентацию и код, пожалуй, выложу следующим постом.
Passed last week # ЗПШ_SPБГУ for me, perhaps, was the best of all, which I visited. Partly because I myself decided to approach my lecture "scientifically": I chose a topic at the intersection of psychology, mathematics and finance, and even tried to reproduce the effect of "underreaction / overreaction" (Barberis et al., 1998), for which I conducted a mini -experiment. If you have not completed this survey, I advise you to pass it (bit.ly/pgi-math): it is short, and it will be more interesting to read further.
The introductory text for the survey looks like.
I have two coins. The first (let's call it eagle-oriented) falls in an eagle in 70% of cases, tails in 30%. The second one is lattice-oriented - exactly the opposite: 70% tails, 30% is an eagle.
I hide the coins and choose one of them at random. I will give this coin and report the results to you. The remaining non-selected coin in the experiment is no longer involved.
At each step, I report the result of the next shot. Your task: to estimate the probability that I throw up an eagle-oriented coin.
Next, the results of the shots are consistently reported to the participant or participant. This is series 1: eagle, 2: eagle, 3: eagle, 4: eagle, 5: eagle, 6: tails.
The text also states that there is no concept of “wrong” evaluation, since the evaluation procedure is a subjective process. If we were absolutely rational, we would first choose the assessment procedure (optimal in some strictly defined sense), and then use it without changing it with another when new information comes. One of such methods of estimation is the use of the Bayes formula. Bayesians reason like this: if there were no popping up yet, then the odds are 50 to 50. If there are much more eagles in the series of popping up, for example, 3 eagles and not a single tail, will the eagle-orientation be still 50%? No, because such an outcome of the experiment is more likely for an eagle-oriented coin, rather than for a tail-oriented one. Thus, the greater the imbalance between the number of eagles and tails, the more we can be sure which coin was chosen. (If this argument is not convincing, try replacing 70% / 30% with 99% / 1% for both coins and repeating the reasoning.)
This reasoning consists in the essence of the Bayesian formula: the probability of an event occurring under the condition that the information P (A | B) is expressed is P (B | A) * P (A) / P (B). Here, in our case, A means the event "eagle-oriented orientation of a randomly selected coin," B - the "history of the observed throws" (it changes at each experiment step). The rest is a matter of technique. The derivation of the formula in general form for n eagles and m tails is quite simple, especially considering that P (A) = 0.5. I will give the final result: P (A | B) = 0.7 ^ n * 0.3 ^ m / (0.7 ^ n * 0.3 ^ m + 0.7 ^ m * 0.3 ^ n). The use of this formula gives the answers to the “fully rational Bayesian”: 70%, 84.5%, 92.7%, 96.7%, 98.6%, 96.7%.
Well, now look at the experimental data! Each black trajectory indicates one series of answers. If the paths overlap, the line becomes less transparent. Three categories of answers are most popular: all estimates are 50% (new information does not affect in any way), all estimates are 70% (apparently, only the fact that there are more eagles), as well as Bayesian estimation (this group used the Bayes formula it is very difficult to get into this trajectory without calculation). Well, on average (blue), estimates are similar in form to Bayesian, but they are greatly underestimated. This can be conditionally described as an underreaction effect. If you look at the average, excluding the trajectories "all 50%" / "all 70%" (orange), then here the confidence interval with a confidence level of 99% covers the Bayesian trajectory. The overreaction effect, to which the authors of the original article are appealing, could not be found. Science is hard!
Links to the presentation and the code, perhaps, lay the next post.
The introductory text for the survey looks like.
I have two coins. The first (let's call it eagle-oriented) falls in an eagle in 70% of cases, tails in 30%. The second one is lattice-oriented - exactly the opposite: 70% tails, 30% is an eagle.
I hide the coins and choose one of them at random. I will give this coin and report the results to you. The remaining non-selected coin in the experiment is no longer involved.
At each step, I report the result of the next shot. Your task: to estimate the probability that I throw up an eagle-oriented coin.
Next, the results of the shots are consistently reported to the participant or participant. This is series 1: eagle, 2: eagle, 3: eagle, 4: eagle, 5: eagle, 6: tails.
The text also states that there is no concept of “wrong” evaluation, since the evaluation procedure is a subjective process. If we were absolutely rational, we would first choose the assessment procedure (optimal in some strictly defined sense), and then use it without changing it with another when new information comes. One of such methods of estimation is the use of the Bayes formula. Bayesians reason like this: if there were no popping up yet, then the odds are 50 to 50. If there are much more eagles in the series of popping up, for example, 3 eagles and not a single tail, will the eagle-orientation be still 50%? No, because such an outcome of the experiment is more likely for an eagle-oriented coin, rather than for a tail-oriented one. Thus, the greater the imbalance between the number of eagles and tails, the more we can be sure which coin was chosen. (If this argument is not convincing, try replacing 70% / 30% with 99% / 1% for both coins and repeating the reasoning.)
This reasoning consists in the essence of the Bayesian formula: the probability of an event occurring under the condition that the information P (A | B) is expressed is P (B | A) * P (A) / P (B). Here, in our case, A means the event "eagle-oriented orientation of a randomly selected coin," B - the "history of the observed throws" (it changes at each experiment step). The rest is a matter of technique. The derivation of the formula in general form for n eagles and m tails is quite simple, especially considering that P (A) = 0.5. I will give the final result: P (A | B) = 0.7 ^ n * 0.3 ^ m / (0.7 ^ n * 0.3 ^ m + 0.7 ^ m * 0.3 ^ n). The use of this formula gives the answers to the “fully rational Bayesian”: 70%, 84.5%, 92.7%, 96.7%, 98.6%, 96.7%.
Well, now look at the experimental data! Each black trajectory indicates one series of answers. If the paths overlap, the line becomes less transparent. Three categories of answers are most popular: all estimates are 50% (new information does not affect in any way), all estimates are 70% (apparently, only the fact that there are more eagles), as well as Bayesian estimation (this group used the Bayes formula it is very difficult to get into this trajectory without calculation). Well, on average (blue), estimates are similar in form to Bayesian, but they are greatly underestimated. This can be conditionally described as an underreaction effect. If you look at the average, excluding the trajectories "all 50%" / "all 70%" (orange), then here the confidence interval with a confidence level of 99% covers the Bayesian trajectory. The overreaction effect, to which the authors of the original article are appealing, could not be found. Science is hard!
Links to the presentation and the code, perhaps, lay the next post.
У записи 24 лайков,
0 репостов,
680 просмотров.
0 репостов,
680 просмотров.
Эту запись оставил(а) на своей стене Антон Антонов









































